- Published on
Lineer Regresyon Nedir? Nasıl Kullanılır? [Detaylı ve Anlaşılır Örneklerle]
- Authors

- Name
- Alperen Önal
Lineer regresyon, makine öğrenmesinde kullanılan en temel ve yaygın yöntemlerden biridir. Amaç, bir bağımlı değişken(y) ile bir veya daha fazla bağımsız değişken(x) arasındaki ilişkiyi doğrusal olarak modellemektir. Yani verilerin arasındaki ilişki bir doğru ile ifade ederek varsayım yapıyoruz. Lineer regresyon 2'ye ayrılmaktadır:
Basit Lineer Regresyon:
- Yalnızca bir adet bağımsız değişken kullanır.
- Örneğin: Bir kişinin boyunu tahmin ederken sadece yaş değişkeninden faydalanıyorsak, bu bir basit lineer regresyon örneği olacaktır.
- Matematiksel gösterimi, = + x şeklindedir.
Çoklu Lineer Regresyon(Multiple Linear Regression):
- Birden fazla bağımsız değişken kullanır.
- Örneğin: Bir kişinin boyunu tahmin ederken yaş, kilo vb. değişkenlerden faydalanıyorsak, bu bir çoklu lineer regresyon örneği olacaktır.
- Matematiksel gösterimi, şeklindedir.
Veya hipotez fonksiyonumuzu(h) genel olacak şekilde şöyle ifade edebiliriz:
- where = 1
- Böylece her iki lineer regresyon çeşidi için de matematiksel ifademizi gerçekleştirmiş oluruz.
- = 1 yapıyoruz çünkü basit lineer regresyonun temsilini de sağlamak istiyoruz.
Buradaki j ne? n ne? gibi soru işaretlerini gidermek için terminolojimize göz atalım:
Terminoloji
- h(x) -> modelin tahmin fonksiyonudur. Başka bir deyişle hipotez fonksiyonumuzdur.
- h(x) = = ŷ, bunların hepsi aynı şeyi ifade eder.
- Şekil 1. için = + x (basit lineer reg. çünkü 1 feature var.)
- Veya daha genel bir gösterim olan: where = 1
- -> Parametrelerimiz(coefficient).
- Amacımız her zaman bu değeri en uygun olacak şekilde seçmek. Bunun nedenini ve nasıl seçeceğimizi daha sonra öğreneceğiz.
- m -> training örneklerimizin sayısı(veri setindeki satır sayısı)
- Şekil 1. için m=10
- x -> inputs veya başka bir deyişle features yani etiket sütunu haricinde kalan verilerimiz.
- Şekil 1. için x = [11, 8, 17, 15, 12, 17, 9, 11, 14, 7]
- y -> output veya başka bir deyişle target variable yani etiket sütunumuz.
- Şekil 1. için y = [145, 123, 177, 167, 149, 182, 135, 146, 171, 129]
- n -> özellik(features)'lerin sayısı
- (x, y) -> traning örneğimiz
- -> training eğitim veri noktası.
- Şekil 1. için ve i=1 olmak üzere => (, = (11, 145)
- Şekil 5. için ve i=1 olmak üzere => (, = ([11, 59.7], 145)
- Buradaki i'lerimiz, üslü gösterimiyle karıştırılmamalıdır.
- Buradaki ifademiz, i. veri noktasının giriş(input/features) vektörüdür.
- Eğer özellikler tek bir değer değil birden fazlaysa (örneğin , , ), bu bir vektör(features vector) olarak yazılabilir:
- Örneğin, 1. özelliğin(features) 1. değerini döndürür. (programlamadaki karşılığı: array[0][0])
- -> training eğitim veri noktası.
Lineer Regresyon Parametrelerin Bulunması
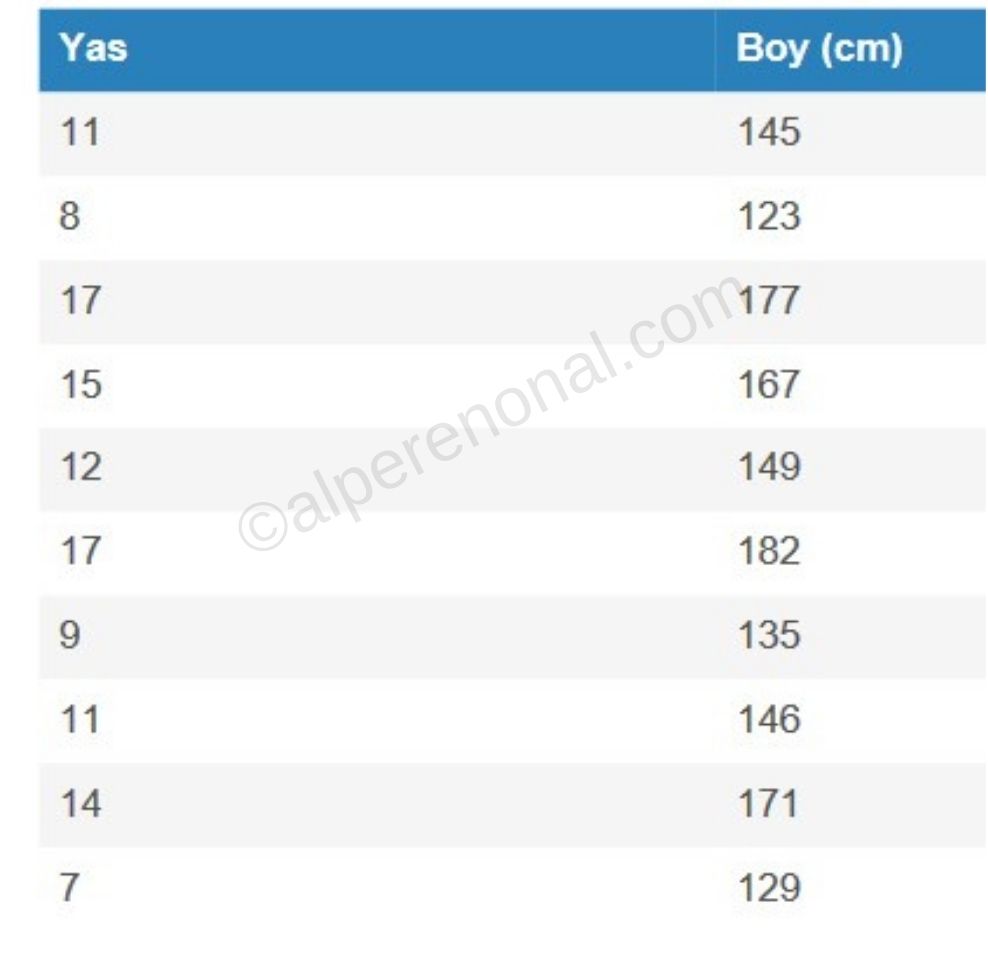
Şekil 1. Türkiye'deki insanların yaşlarına göre boy uzunluklarını içeren veri seti.
Örneğin Şekil 1.'deki tabloyu yas bağımsız değişken(x), boy bağımlı değişken(y) kabul ederek çizecek olursak:
Yaş ve Boy Dağılımı:
Şekil 2. veri setimizdeki veri noktalarının dağılım grafiği.
Şimdi bu grafikteki amacımız tüm veri noktalarına en iyi oturacak şekilde bir doğru çizmek. Böylece ileride gelecek değerlerin tahminini gerçekleştirebiliriz.
Basit reglesyon için formülümüzü hatırlayalım: ℎ(x) = + x
Şimdi, bu doğruyu çizebilmek için , parametrelerine ihtiyacımız var.
- = y eksenini kestiğimiz nokta.
- = eğimimiz(slope)
Bu doğruyu, göz kararı Şekil 3.'deki gibi tüm veri noktalarına en yakın olacak şekilde çizebilirim. Örneğin:
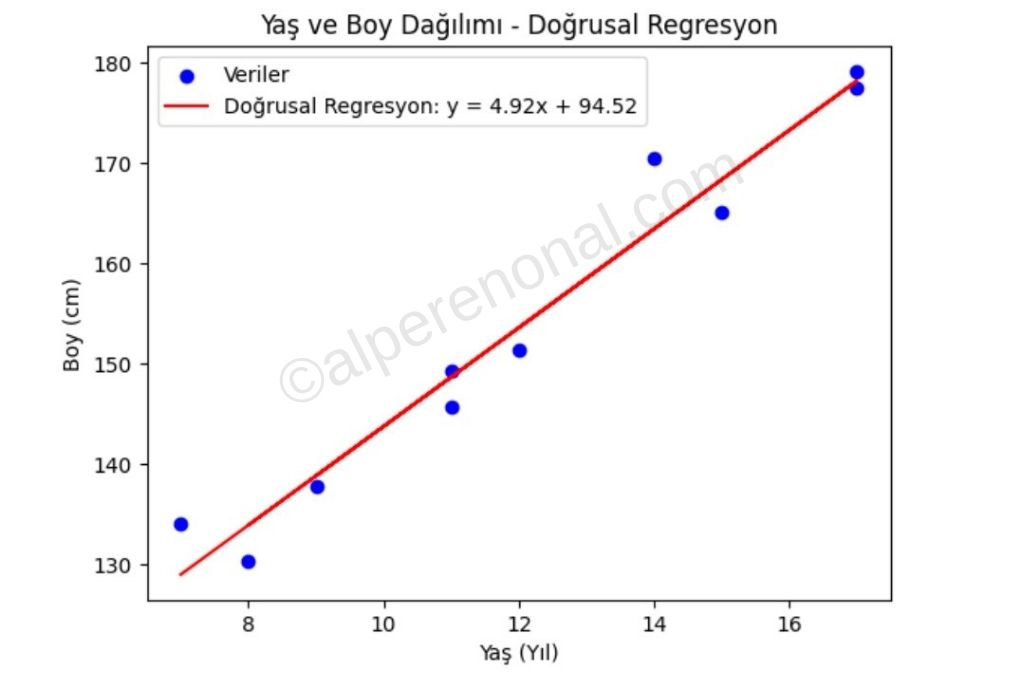
Şekil 3. lineer regresyon doğru çizimi.
Göz kararınca kafamdan uydurduğum bu doğrunun parametrelerini, yani , değerlerini görebiliyoruz ( = 94.52, = 4.92).
Ancak böyle bir şey yaparsam lineer regresyon modelimin doğruluk oranı beklenenden düşük olabilir. Yani, , parametrelerinin 94.52 ile 4.92 değerleri için en iyi doğruluk oranına sahip doğruyu verdiği büyük bir soru işareti. Bu yüzden parametrelerimizi seçmek için bazı yöntemleri kullanmak zorundayız. Lineer regresyonda kullanılan yöntemlerden olan Ortalama Kareler Hatası(MSE, mean squared error) ve Ortalama Mutlak Değer hatası(MAE,mean absolute error) inceleyelim.
Mean Squared Error
Ortalama Kareler Hatasını(MSE, mean squared error), kullanma amacımız üstteki yazıda da belirttiğimiz gibi, parametrelerimizi( , , ..., ) verisetimize en uygun şekilde seçerek, yüksek doğruluk sunan bir doğru edinmek.
Örneğin Şekil 4.'deki tahmin değeri(ŷ) ve gerçek değer(y)'i birbirlerinden çıkartırsak yaş 14 için() hata oranını buluruz.
- ŷ-y = hata oranı olduğuna göre => 161 - 171 = -10 çıkar. Yani, için -10'luk bir hatamız var.
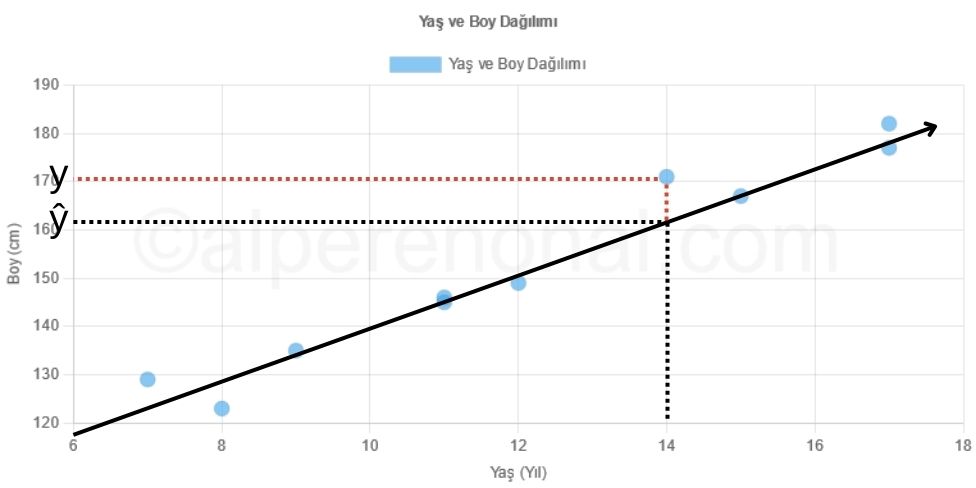
Şekil 4. Lineer regresyon hata oranı
Hatanın nasıl bulunduğunu artık biliyoruz. Şimdi toplam hatayı bulalım:
- ŷ'nin, h(x) ile aynı şey olduğunu hatırlayalım.
- Neden karesini aldık? Çünkü hatamızın negatif olmasını istemiyoruz. Örneğin: 2 satırdan oluşan verisetimiz için çizdiğimiz doğruda ilk hatamız -1 çıktı ikinci hatamız 1 çıktı diyelim, 1-1=0 yani bizim toplam hatamız 0 mı? Hayır, kesinlikle değil. Bu yüzden hataları toplarken negatif değer olmasını istemiyoruz. Tabii ki bunun için mutlak değer de kullanabilirdik(MAE) ancak hatanın karesini alarak modelimizi, çıkan her hata için o hatanın karesi kadar ek ceza veriyoruz. Zaten, yöntemin adı da buradan geliyor.
- Özetle, Şekil 4.'deki veri noktası için bulduğumuz hatayı, her bir veri noktamız için bulup karelerini aldık ardından topladık.
Toplam hatayı da artık biliyoruz son olarak ortalama hata değerimizi bulalım:
- m'ye yani, verilerimizin bulunduğu satırların toplamına bölersek ortalamayı elde ederiz:
🥳Tebrikler, MSE(Mean Squared Error) formülünü elde ettik:
Tekrar üstünden geçelim; amacımız, bu MSE değerini olabildiğince düşük tutan parametrelerimizi( , , ..., ) bularak doğrumuzu çizmek. Böylece, en düzgün doğruyu elde edebiliriz.
MAE(mean absolute error)
Yukarıdaki adımları aynen uyguluyoruz ancak kare alma işlemini uygulamak yerine mutlak değerini alarak toplam hatayı buluyoruz.
MAE(mean absolute error) ve Mean Squared Error(MSE) Farkları Nedir? Hangisi Kullanmalıyız?
- MSE'de her hatanın karesini alarak modeli ek olarak cezalandırılmasını sağlıyoruz ve hata toplamının yanlış çıkmamasını sağlıyoruz.
- MAE'de her hatanın mutlak değerini alarak hata toplamının yanlış çıkmamasını sağlıyoruz. Ancak ek bir ceza yazmıyoruz, sadece toplam hata neyse cezamız o oluyor.
- Genellikle ceza olan bahsedilen şey şudur: doğruluktan ne kadar uzak olduğumuz, modelimizin ne kadar hatalı çalıştığıdır. MSE, MAE gibi yöntemlerle ne kadar ceza keseceğimizi buluyoruz diyebiliriz.
- Genellikle cost function(maliyet fonksiyonu)'una yakınlığı nedeniyle MSE kullanılmaktadır.
- Hangisini kullanacağımıza gelecek olursak, bunun tam bir cevabı yok. İhtiyaca göre 2'si de kullanılabilir ama az önce belirttiğim gibi genellikle MSE kullanılıyor.
Lineer Regresyon Örnek
Şekil 1.'deki veri setinde 1 özelliğimiz(feature) vardı.Şekil 5.'de bir de kilo özelliğini ekledik. Artık 2 özelliğimiz var. Ve artık bu 2 özelliği kullanarak, output'umuzu(y) bulmak istediğimizi farz edelim. Artık, basit lineer regresyon kullanamayız çünkü 1'den fazla özelliğimiz var. Çoklu lineer regresyon kullanacağız.
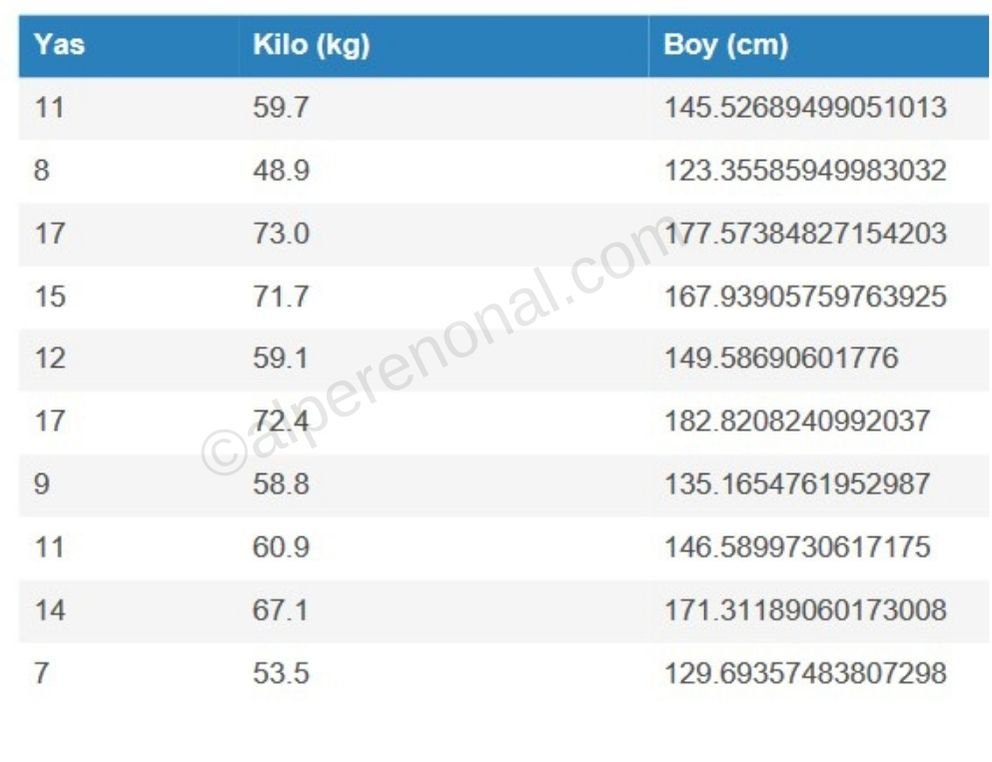
Şekil 5. Türkiye'deki insanların yaşlarına ve kilolarına göre boy uzunluklarını içeren veri seti.
Çoklu doğrusal regresyon'da bir tane bağımlı ve birden fazla bağımsız değişken kullanılarak grafik çizilir. Yani Şekil 5.'deki veri setimiz için, Şekil 3.'deki gibi 2 boyutlu bir grafik yerine Şekil 6.'deki gibi 3 boyutlu bir grafiğimiz olucak.
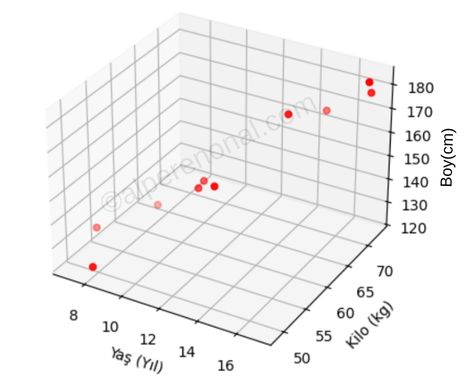
Şekil 6. çoklu lineer regresyon veri dağılımı.
Şekil 6.'de görülebileceği gibi 2 bağımsız değişkenimiz(yaş, kilo) ve 1 bağımlı değişkenimiz(boy) var.
Evet basit lineer regresyonda olduğu gibi bu veri setimiz için de kafama göre bir doğru oluşturup göz kararınca veri noktalarından geçirmeye çalışacağım ve neye benzediğini göreceğiz.
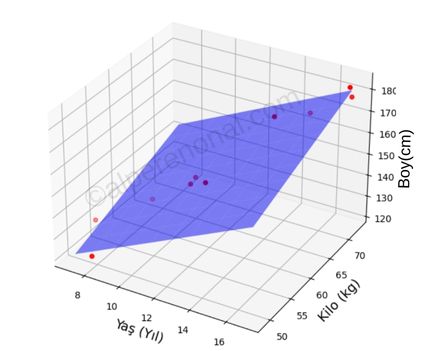
Şekil 7. çoklu lineer regresyon doğru uydurma örneği.
Bu modelimizin denklemi: şeklinde olacaktır.
Bu yazımızda, lineer regresyon kavramını detaylı bir şekilde ele aldık. Basit ve çoklu lineer regresyonun ne olduğunu, matematiksel temellerini, parametrelerini ve kullanım alanlarını öğrendik. Ayrıca, hata ölçümleri (MSE ve MAE) ve bu yöntemlerin nasıl uygulanabileceğini de açıkladık.
Umarım faydalı olmuştur. Yazının uzun olmaması ve amacından çıkmaması için; doğrumuzun parametrelerinin, bulunmasına bir sonraki yazılarımızda değineceğim. Bir sonraki yazımızda görüşürüz 👋👋👋🤙 (4:30)
Bu konun devamı için tıklayın : Maliyet Fonksiyonu ve Fonksiyonun Parametrelerin Bulunması?