- Published on
KNN Algoritması Nedir?
- Authors

- Name
- Alperen Önal
KNN(K-Nearest Neighbors), Türkçe adıyla K-En Yakın Komşu,hem sınıflandırma hem de regresyon problemleri için kullanılan basit ve etkili bir supervised makine öğrenmesi algoritmasıdır.
Temel Mantığı
- Yeni bir veri noktasını, eğitim veri setindeki en yakın k komşularına bakarak sınıflandırmak veya tahmin etmektir.
- "Benzer şeyler birbirlerine yakındır(feature simulatirty)" prensibine dayanmaktadır.
Kullanım Senaryoları
- Etiketli ve küçük veri setlerinde kullanılmaktadır.
- Büyük veri setlerinde kullanılması mantıklı değildir.
Nasıl Çalışır?
Mesafe Hesaplama:
- Input olarak alınan yeni veri noktası ile eğitim veri setindeki her bir nokta arasındaki mesafe hesaplanır.
- Mesafenin hesaplanması için veri seti içeriğine göre farklı mesafe metrikleri kullanılmaktadır:
- Öklid Mesafesi(Euclidean)
- Manhattan Mesafesi
- Minkowski Mesafesi
- ...
En Yakın Komşunun Seçilmesi:
Mesafenin en kısa olduğu hangi kaç en yakın komşuya bakılacağını belirleyen k nokta belirlenir.
k değeri, beraberlik sorunlarının önüne geçmek için tek sayı olarak seçilmelidir.
k değerini belirlemek modelin performansını ve doğruluğuna direkt etki edeceği için önemli bir hiperparametredir. K değerinin nasıl seçilmesi gerektiği, veri setinin yapısına, problemin türüne ve hedeflenen doğruluk oranına bağlı olarak değişiklik göstermektedir.
- Küçük k değeri = daha az karmaşık model = overfitting(aşırı öğrenme) riski
- Büyük k değeri = daha fazla karmaşık model = underfitting(eksik öğrenme/genelleme yapma) riski
k değerinin en uygun belirleme işlemine hiperparametre optimizasyonu(hyperparameter optimization) denilmektedir.
Sonucun Elde Edilmesi:
- Sınıflandırma: En yakın k adet komşunun sınıfları arasında çoğunluk oylaması yapılır ve yeni veri noktası bu oylamayı kazanan sınıfa atanır. - Regresyon: En yakın k adet komşunun hedef değerlerinin ortalaması alınır ve yeni veri noktası için bir tahmin yapılır.
KNN Örneği:
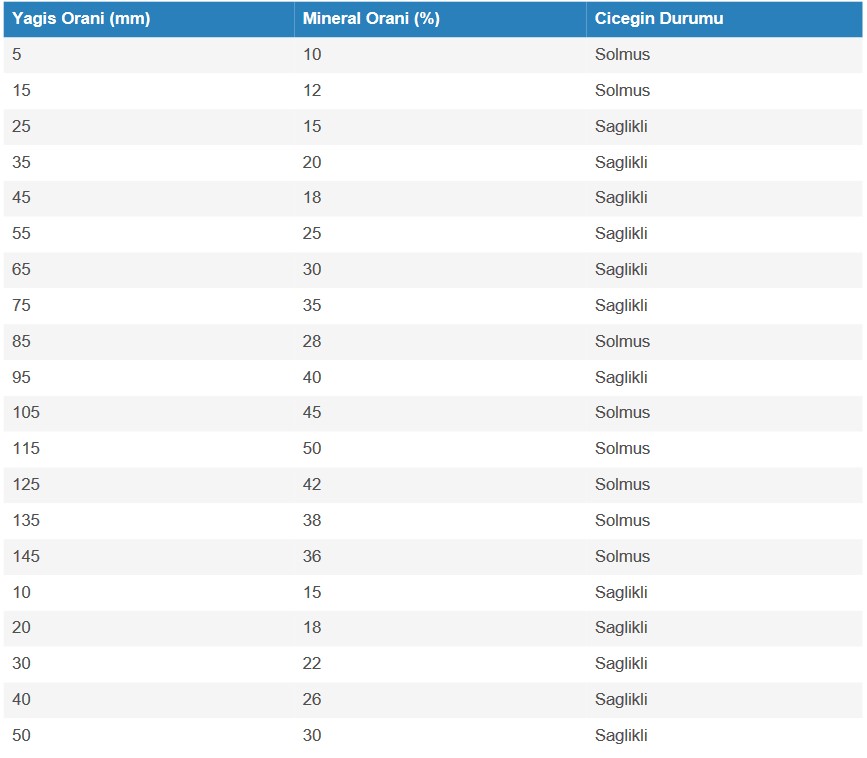
20 satırdan ve 3 (2 numerik + 1 etiket) sütundan oluşan çiçeğin(gül) 30 gün içerisinde solup solmadığını gösteren veri seti.
Örneğin yukarıdaki gibi etiketli olan bir veri setimiz olsun. Amacımız, bir sonraki verinin hangi sınıfa dahil olduğunu bulmak olsun. Başka bir deyişle elimize aynı türden bir çiçeğin mineral oranı ve yağış oranı özellikleri gelcek ve biz de bu çiçeğin 30 gün içerisinde solup solmayacağını tahmin edeceğiz.
KNN Sınıflandırma Grafiği(Features ekseninde)
Problem: Bu gül 30 gün içerisinde solacak mı? Solmayacak mı?
Elimize bir gülün değerleri geldi:- Yeni değerler: yağış(x) oranı = 50, mineral(y) oranı = 25
Her bir veri noktası için öklid uzaklıklarını hesaplarız:
Örneğin ilk 2 satır için hesaplamak istersek:
- Veri Noktası (X₁): (5, 10)
Formül:
Hesaplama:
- Veri Noktası (X₂): (15, 12)
Formül: Hesaplama:
Bu işlemleri tüm veri noktalarımız için uygulayacak olursak:
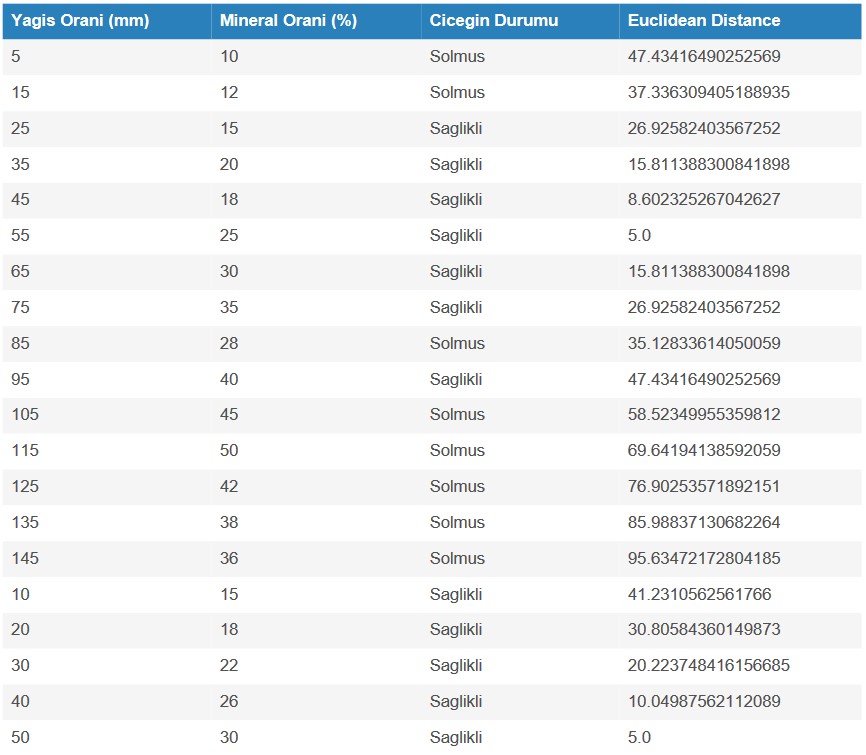
Yeni verimiz için veri setimizdeki tüm veri noktalarına olan öklid mesafeleri.
Örneğin k=3 değeri için; 5.satır'daki veri noktamız, 6.satır'daki veri noktamız ve 20. satırdaki veri noktamız oylamaya katılacaktır.
KNN Grafiği (k = 3)
Grafikten de görebileceğimiz gibi bu en yakın 3 veri noktamız sağlıklı sınıfına ait olduğu için yeni verimizi de sağlıklı olarak kabul edebiliriz.
Problem 2: Bu gül 30 gün içerisinde solacak mı? Solmayacak mı?
Elimize bir gülün değerleri geldi:- Yeni değerler: yağış(x) oranı = 68.33, mineral(y) oranı = 28.56
Her bir veri noktamız için öklid mesafelerini bulacak olursak :

Yeni verimiz için veri setimizdeki tüm veri noktalarına olan öklid mesafeleri(Yeni değerler: yağış(x) oranı = 68.33, mineral(y) oranı = 28.56).
k=3 değeri için; 1. satır'daki veri noktamız, 16. satır'daki veri noktamız ve 17. satırdaki veri noktamız oylamaya katılacaktır.
KNN Grafiği (Yeni Nokta, k = 3)
Sonuç: Grafikten de görülebileceği gibi k=3 için oylamaya katılan 2 veri noktamız solmuş sınıfına ait iken 1 veri noktamız sağlıklı sınıfına aittir. Bu yüzden çoğunluğa uyarak, bu yeni veri noktamız da Solmuş sınıfına ait olduğunu buluruz.
Jupyter Notebook Üzerinden Örnek
Aynı Veri setimizi kullanarak yeni değerleri: yağış(x) oranı = 15.0, mineral(y) oranı = 12.5 olan gül için tespitte bulunacak olursak.
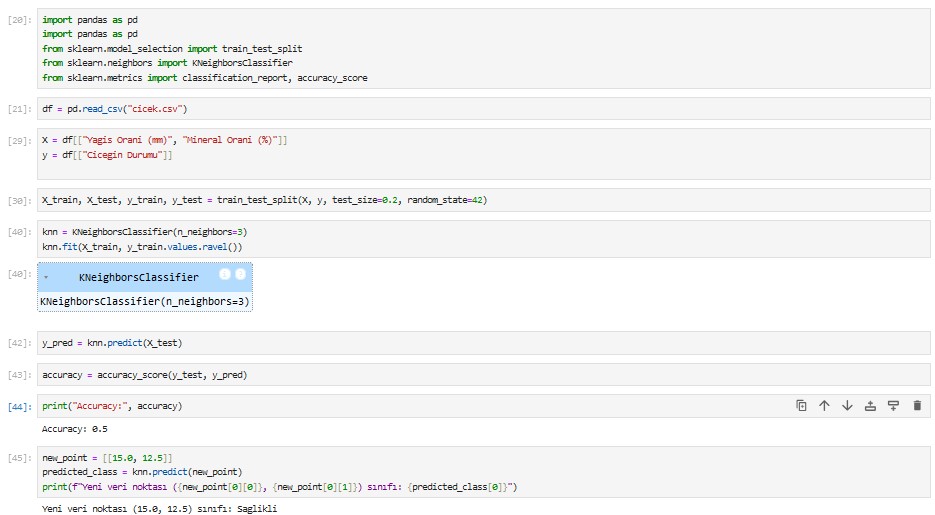
jupyter notebook'da KNN örneği.
Okuduğunuz için teşekkürler, bir sonraki yazıda görüşmek üzere.
